D:音乐题,如果学过吉他,可能比较容易理解题意:
吉他第i弦的第j品的音调为i弦的空弦音+j,给n(≤1e5)个弦的空弦音,有q(≤1e5)个询问,每次求所有弦第l品到第r品(0≤l≤r≤1e18)共能表示多少个音。
首先显然要把弦按空弦音升序排序。每次覆盖时,答案显然只和(r-l+1)有关。所以不妨把l统一设成0,对每根弦每次覆盖到的区间是[0,r-l]。这样就可以把每根弦的空弦音放在一根数轴上,对每个节点覆盖长为(r-l+1)的区间,答案就是被覆盖到的区间总长度。图为样例一的第二问,区间长度为(2-0+1)=3。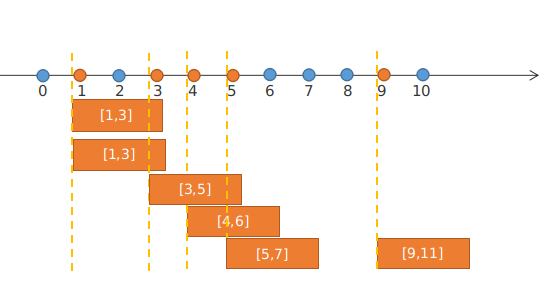
我们可以发现,如果某个区间长度大于相邻两个点的距离,那么区间大于该距离的部分一定会被后一个区间“截掉”(如图中的1和3距离为2,小于当前区间长度3,所以以1开始的区间[1,3]的部分被后面的[3,5]覆盖;类似的,区间[3,5]又有一部分被[4,6]覆盖等)。只有长度小于相邻两个点距离的区间得到完整的保留。由于被截掉的区间相当于只剩下相邻两点距离的长度,因此所有部分被截掉的区间长度和就是所有这些相邻点距离的和。因此可以分别统计“部分被截断的区间总长度”和“全部保留的区间总长度”。只要找到所有长度小于询问区间长的相邻点距离并求和,再加上剩余未被截断的区间总长度就是答案。所以可以预处理相邻点的距离,并将它们从小到大排序,求出前缀和,就可以按每个询问的区间长二分查找,快速求出符合要求的区间长度和。未被截断的区间更好处理,求出总数量后乘区间长度即可。
(所以从代码上看就是各种排序+差分+前缀和……)
1 |
|
另一种思路是离线处理,将询问按区间长从小到大排序,再利用单调性求出答案,同样要各种差分排序……在此不再赘述,可以参考zyp巨佬的代码。
E:贪心乱搞题。有a[i]个长度为$2^i$的火柴,问这些火柴总共能构成多少个三角形?
显然,每个三角形必须由两根长度为$2^i$和一根长度为$2^j$的火柴构成,其中j<=i。
这句话显而易见,但只要意识到这句话的正确性,答案也就呼之欲出了!
考虑哪些火柴是不能用来组成三角形的:对于每一种长度,如果它有奇数个火柴,且没有两根长度相等且大于等于它的长度的火柴来跟他匹配,那么这根火柴相当于作废。
所以按长度从大到小遍历各种火柴,先不急着拼出三角形,而是让火柴成对匹配,实时统计长度大于等于i的成对火柴数,如果某根火柴不能成对,即当前长度的火柴数量为奇数,那么需要消耗一组长度大于等于它的成对火柴来跟他形成三角形。如果当前没有成对火柴,却有单独的火柴,那么这一根单独的火柴就作废了。
这样扫一遍,可能还会剩下一堆成对火柴没有拼成三角形,但显然可以拆掉若干对长度较小的火柴来和长度较大的成对火柴拼成三角形。所以直接把没有作废的火柴数量整除3就得到答案了。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
using namespace std;
typedef long long ll;
int a[402000],b[402000];
int main (/*int argc, char const* argv[]*/){
std::ios::sync_with_stdio(false);
int n;cin>>n;
ll w=0,s=0;
for(int i=1;i<=n;i+=1){
cin>>a[i];
s+=a[i];
}
int t=0,bd=0;
for(int i=n;i>=1;--i){
t+=a[i]/2;
if(a[i]%2){
if(!t)++bd;
else --t;
}
}
cout<<(s-bd)/3<<endl;
return 0;
}
以上。