上紫~
其实感觉这次比赛,最坑的还是C题……虽然本菜最后乱猜瞎搞,算是搞出来了,也能大概说明理由,但Acoder巨佬告诉我们有结论可以用,所以还是等他的题解吧……
但是D和E其实完全都是可做的,难度并不高,而在比赛时做出来的人很少。考场上,真正被题目打倒的,有时还没被吓死的人多。
D:给一个n(n≤1000),得到所有由n对匹配括号构成的字符串(显然每个字符串长度为2n),设一个字典树仅包含所有这样的字符串,并设定一个集合,这个集合包含这棵字典树的若干条边,且集合中任意两条边没有公共点。求这个集合中元素数量的最大值。
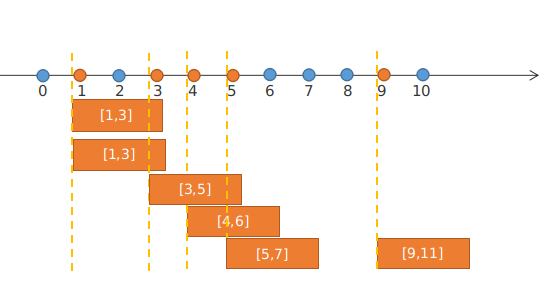
这道题题意描述相当绕……观察一下题目下方的字典树,从底向上看,对相邻的两层边,显然取底部的一条边一定不会比取它上方的一条边劣,而一旦取了下层的某条边,其上方相连的边就不能取了,因为这两条边共用了一个节点。所以不妨取最下方一层边,倒数第三层边,倒数第五层……又由于同一层的边也不能共用节点,所以实际能取的边数相当于倒数第二层节点,倒数第四层节点,倒数第六层节点……的数量和。
那么如何求每一层节点的数量呢?其实,看到括号匹配,我们一般会想到先把n对括号匹配形成字符串的总数量求出来。由于n不超过1000,以及状态可以很容易地表示,考虑$n^2$的dp。由于每个位置选择括号的方案数只与之前两种括号各自的数量和可行的方案数有关,而与其排列无关,设f[i][j]表示前i个括号中有j个左括号的方案数(注意j的范围:显然j的数量不能多于n,但也不能少于i/2+i%2,否则当前左括号数量少于右括号数量,即当前方案非法。这样可以确保非法字符串方案数为0),分当前括号是左括号还是右括号两种情况进行转移。由于确保非法的方案数为0,所以不会出现非法方案转移出合法方案的bug。
转移方程:
$f[i][j]=f[i-1][j-1]+f[i-1][j],(i//2+i\%2≤j≤n)$(部分杨辉三角???)
也不需要啥优化了……很简单的方程。
所以我们发现,在求总方案数时,字典树每层节点数量也顺便求出来了!因为第i层节点数就是前i个括号的总方案数,也就是f[i][1]~f[i][n]的和。按照最开始的贪心策略,随便统计一下就解决啦。
考场上这道题只有360人做出来,但回过头看这道题,其实难度并不大,只是一个很明显的贪心和很简单的dp就出来了。估计大家都被C题搞蒙了,然后看到D题绕来绕去的描述还有可怕的字典树,直接吓跑了……
代码也非常简单:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
using namespace std;
typedef long long ll;
ll f[4020][4020];
const ll p=1000000007;
int main (/*int argc, char const* argv[]*/){
std::ios::sync_with_stdio(false);
std::cin.tie(0);
int n;cin>>n;
f[0][0]=1;
for(int i=1;i<=n*2;i+=1){
for(int j=i/2+i%2;j<=n;j+=1){
f[i][j]=f[i-1][j-1]+f[i-1][j];
f[i][j]%=p;
}
}
ll ans=0;
for(int i=n*2-1;i>=1;i-=2){
for(int j=1;j<=n;j+=1){
ans+=f[i][j];
ans%=p;
}
}
cout<<ans<<endl;
return 0;
}
E题就更惨了……考场上只有34人做出来(当然本菜当时也没做出来,考完回头一看才明白……)。题目描述同样很绕:有一组数a,定义b[i]=min(a[i],a[i+1]),c[i]=max(a[i],a[i+1]),然后打乱b和c的顺序得到b’和c’,但是对每个i,b[i]和c[i]的相对位置不变,即:如果b[i]->b’[j],那么c[i]->c’[j] (原题目描述还要绕,搞了一个排列来表示对应关系,但实际就是这个意思)。现在给了b’和c’,求原来的a是否存在,如果存在,求出任意一个可能的a。
根据题目描述,b[i]=min(a[p],a[p+1]),c[i]=max(a[p],a[p+1]),也就意味着b[i]和c[i]在原数组相邻,但先后顺序未知。这样得到n-1组相邻关系。那么如何用这样的相邻关系得到原数组呢?如果把每一个数字当做一个节点,在相邻的两个数字之间连一条边,可以发现,从某个点出发,经过所有的边各一次,遍历到的点按遍历顺序排列(也就是求欧拉路径),就是原来的数组a。由于数字比较大($≤10^9$),所以先离散化,然后就是敲板子了。
如果还不理解……可以看一下洛谷P1341……几乎一样的题,但那玩意还要保证字典序最小……还只是个蓝牌子……
要注意本题可能有大量自环,如果板子不太好,时间复杂度可能直接退化。本菜的板子就有点糟,被卡T了两次,改了半天……
1 |
|
总而言之,卡B卡C,降智打击。所以卡题的时候,一定要敢跳,不然等着冷冰冰……(血泪教训QAQ)
以上。